Class Penalty2DRhomb

• Defined in File PenaltyBarrier2D.hh

Inheritance Relationships

Base Type

• public Mechatronix::Penalty2DTwoCurves (Class Penalty2DTwoCurves)

Class Documentation

class Mechatronix::Penalty2DRhomb : public Mechatronix::Penalty2DTwoCurves

Rhomb type penalty.

Public Functions

inline explicit Penalty2DRhomb(string const &name)

build penalty

virtual void setup(GenericContainer const &vars) override

Initialize the penalty.

The penalty is defined by two level curves, a rhomb and an ellipse. Associative array must contains

• "Xlimit" X ellipse ray

• "Ylimit" Y ellipse ray

• "Xpsy" X rhomb ray

• "Ypsy" Y rhomb ray

• "Epsi" regularizing parameter \( h\)

The ellipse in polar coordinate is given by

\[ r(\theta) = X_{\mathrm{limit}} \cos \theta + Y_{\mathrm{limit}} \sin \theta \]

while the rhomb in polar coordinate is given by

\[ r(\theta) = \frac{1}{\displaystyle\frac{|\cos \theta|}{X_{\mathrm{psi}}} + \displaystyle\frac{|\sin \theta|}{Y_{\mathrm{psi}}}} \]

The absolute value is approximated by \( |a| = \sqrt{h^2+a^2} \). For example with

\[ X_{\mathrm{limit}}=Y_{\mathrm{limit}}=1.6,\qquad X_{\mathrm{psi}}=1.5,\qquad Y_{\mathrm{psi}}=1 \]

results in the following level curve

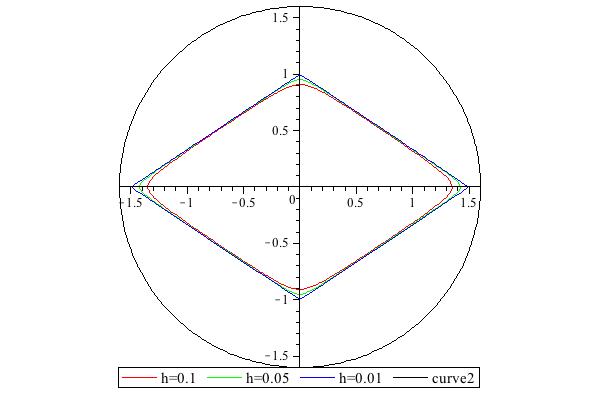
The penalty is 0 inside the rhomb is zero grow quadratically (along the ray). The value of the penalty is 1 on the ellipse level curve.