Class ClipSuperior

• Defined in File RegularizedClip.hxx

Inheritance Relationships

Derived Type

• public Mechatronix::ClipInferior (Class ClipInferior)

Class Documentation

class Mechatronix::ClipSuperior

clip superior class

Subclassed by Mechatronix::ClipInferior

Inizialization

inline explicit ClipSuperior()

void setup(real_type h)

Set h and delta for the approximation of clipped function: \( \min(a,x) \)

\[ \textrm{min}(a,x) = \frac{x+a}{2} -\frac{x-a}{2}\textrm{erf}(\kappa(x-a)) -\frac{\exp(-\kappa^2(x-a)^2)}{2\kappa\sqrt{\pi}} \]

where \( \kappa \) is chosen to satisfy

\[ \min(a,a) = a-h \]

and thus

\[ \kappa = \frac{1}{2h\sqrt{\pi}} \]

void setup(GenericContainer const &gc)

Info

inline void update_h(real_type h)

virtual string info() const

inline void info(ostream_type &stream) const

Evaluate

real_type eval(real_type x, real_type y) const

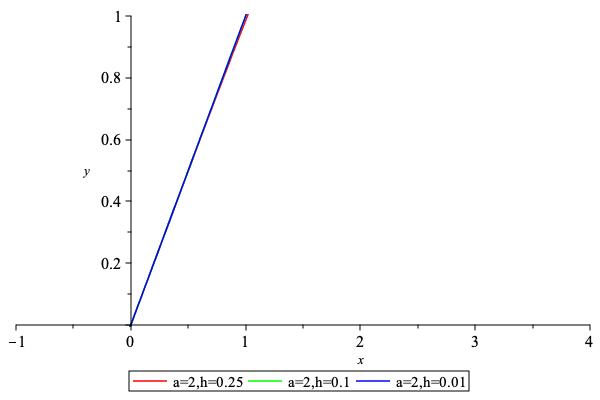
compute clip function \( p(x,y) \)

Evaluate \( \textrm{clip}(x,y) \)

real_type eval_D_1(real_type x, real_type y) const

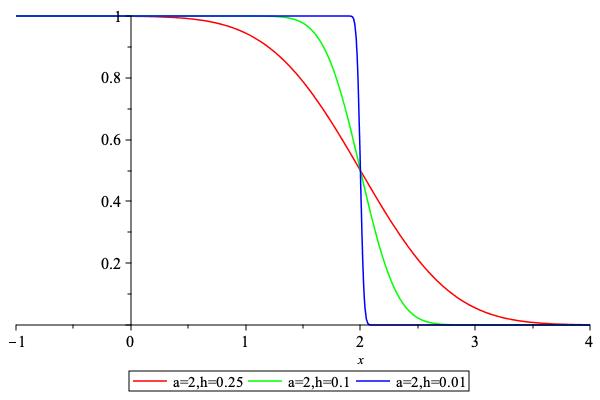
compute clip function partial derivative \( \displaystyle\frac{\partial}{\partial_x} p(x,y) \)

Evaluate \( \displaystyle\frac{\partial}{\partial_x} \textrm{clip}(x,y) \)

real_type eval_D_2(real_type x, real_type y) const

compute clip function partial derivative \( \displaystyle\frac{\partial}{\partial_y} p(x,y) \)

evaluate \( \displaystyle\frac{\partial}{\partial_y} \textrm{clip}(x,y) \)

real_type eval_D_1_1(real_type x, real_type y) const

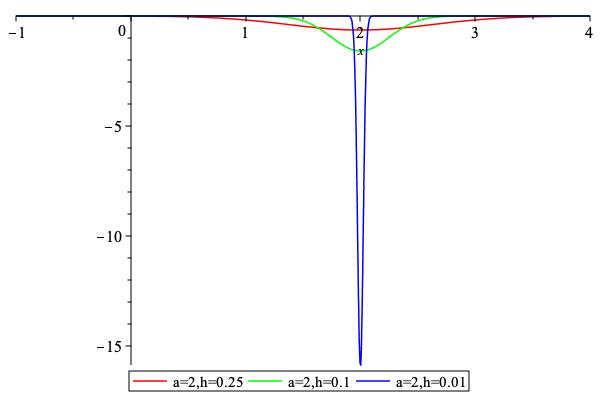
compute clip function partial derivative \( \partial^{(2)}_x p(x,y) \)

Evaluate \( \partial^{(2)}_x \textrm{clip}(x,y) \)

real_type eval_D_1_2(real_type x, real_type y) const

compute clip function partial derivative \( \displaystyle\frac{\partial}{\partial_x}\displaystyle\frac{\partial}{\partial_y} p(x,y) \)

evaluate \( \displaystyle\frac{\partial}{\partial_x}\displaystyle\frac{\partial}{\partial_y} \textrm{clip}(x,y) \)

real_type eval_D_2_2(real_type x, real_type y) const

compute clip function partial derivative \( \partial^{(2)}_y p(x,y) \)

evaluate \( \partial^{(2)}_y \textrm{clip}(x,y) \)

inline real_type operator()(real_type x, real_type y) const

compute clip function penalty \( p(x,y) \)

inline real_type D_1(real_type x, real_type y) const

compute clip function partial derivative \( \displaystyle\frac{\partial}{\partial_x} p(x,y) \)

inline real_type D_2(real_type x, real_type y) const

compute clip function partial derivative \( \displaystyle\frac{\partial}{\partial_y} p(x,y) \)

inline real_type D_1_1(real_type x, real_type y) const

compute clip function partial derivative \( \partial^{(2)}_x p(x,y) \)

inline real_type D_1_2(real_type x, real_type y) const

compute clip function partial derivative \( \displaystyle\frac{\partial}{\partial_x}\displaystyle\frac{\partial}{\partial_y} p(x,y) \)

inline real_type D_2_2(real_type x, real_type y) const

compute clip function partial derivative \( \partial^{(2)}_y p(x,y) \)

Protected Attributes

real_type m_h

real_type m_kappa