Class PenaltyBarrierU_cubic¶
Defined in File PenaltyBarrierU.cc
Inheritance Relationships¶
Base Type¶
public Mechatronix::PenaltyBarrierU_base(Class PenaltyBarrierU_base)
Class Documentation¶
-
class
Mechatronix::PenaltyBarrierU_cubic: public Mechatronix::PenaltyBarrierU_base¶
-
Piecewise cubic penalty.
Public Functions
-
inline explicit
PenaltyBarrierU_cubic(string const &name)¶
-
Construct the penalty.
-
inline virtual void
setup(real_type epsilon, real_type tolerance) override¶
-
Initialize the penalty using the values of \( h \) and \( \epsilon \)
\[ H = 1-h,\qquad A_1 = \frac{2\epsilon}{H},\qquad A_2 = \frac{\epsilon}{H^2},\qquad A_3 = \frac{1-A_2}{h^3},\qquad A_4 = \frac{3(1-A_2)}{h}+2A_2,\qquad A_5 = \frac{3(1-A_2)}{h^2}+A_2,\qquad A_6 = A_2^2-3A_1A_3 \]- Parameters
-
epsilon – [in] value \( \epsilon \)
tolerance – [in] value \( h \)
-
inline virtual real_type
eval(real_type x) const override¶
-
Compute the penalty
\[\begin{split} p(x) = \begin{cases} 1+(A_5\,(x+1)-A_4)(x+1) & x < -1 \\[1em] \epsilon + ((A_2-A_3(x+H))(x+H)-A_1)(x+H) & x\in[-1,-H] \\[1em] A_2\, x^2 & x\in[-H,H] \\[1em] \epsilon + ((A_2+A_3(x-H))(x-H)+A_1)(x-H) & x\in[H,1] \\[1em] 1+(A_5\,(x-1)+A_4)(x-1) & x>1 \end{cases} \end{split}\]where the parameters
\[ H = 1-h,\qquad A_1 = \frac{2\epsilon}{H},\qquad A_2 = \frac{\epsilon}{H^2},\qquad A_3 = \frac{1-A_2}{h^3},\qquad A_4 = \frac{3(1-A_2)}{h}+2A_2,\qquad A_5 = \frac{3(1-A_2)}{h^2}+A_2,\qquad A_6 = A_2^2-3A_1A_3 \]are precomputed after a call of method
setup.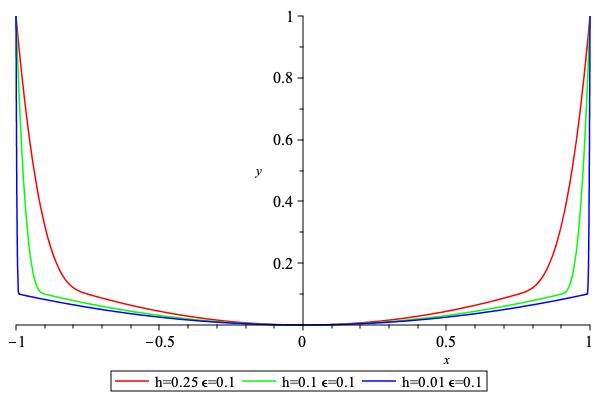
-
inline virtual real_type
solve(real_type RHS) const override¶
-
Solve the problem \( p'(x) = r \)
\[\begin{split} x = \begin{cases} -1 + \frac{r+A_4}{2A_5} & r < -A_4 \\[1em] -H + \frac{r+A_1}{A_2+\sqrt(A_6-3A_3r)} & r < -A_1 \\[1em] \frac{r}{2A_2} & r < A_1 \\[1em] H + \frac{r-A_1}{A_2+\sqrt(A_6+3A_3r)} & r < A_4 \\[1em] 1 + \frac{r-A_4}{2A_5} & \mathrm{otherwise} \end{cases}, \end{split}\]
-
inline explicit