Class PenaltyBarrierU_logarithmic¶
Defined in File PenaltyBarrierU.cc
Inheritance Relationships¶
Base Type¶
public Mechatronix::PenaltyBarrierU_base(Class PenaltyBarrierU_base)
Class Documentation¶
-
class
Mechatronix::PenaltyBarrierU_logarithmic: public Mechatronix::PenaltyBarrierU_base¶
-
Logarithmic barrier.
Public Functions
-
inline
PenaltyBarrierU_logarithmic(string const &name)¶
-
Construct the barrier.
-
inline virtual void
setup(real_type epsilon, real_type tolerance) override¶
-
Initialize the barrier internal parameters based on the values of \( h \) and \( \epsilon \)
for \( h \) and
vars[name()+"Epsi"]for \( \epsilon \)Set the internal parameter
\[ C = \displaystyle\frac{\epsilon}{\log(h(2-h))} \]based on the values of \( h \) and \( \epsilon \)
- Parameters
-
epsilon – [in] value \( \epsilon \)
tolerance – [in] value \( h \)
-
inline virtual real_type
eval(real_type x) const override¶
-
Compute the barrier \( p(x) = C\log(1-x^2) \)
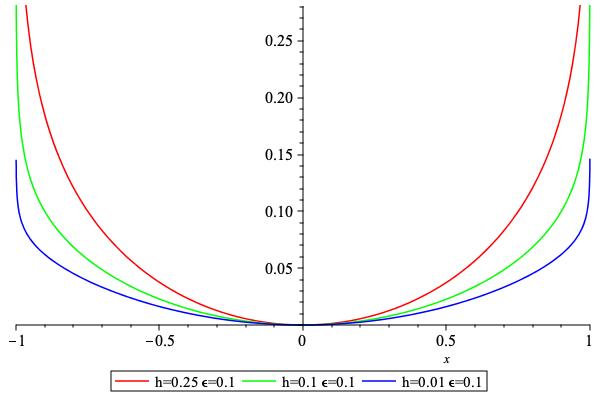
-
inline virtual real_type
eval_DD(real_type x) const override¶
-
Second derivative of the barrierbarrier
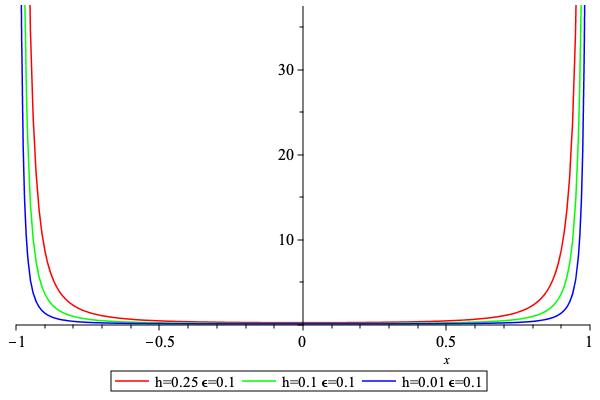
-
inline virtual real_type
solve(real_type RHS) const override¶
-
Solve the problem \( p'(x) = r \). The solution is
\[ x = \frac{r}{\sqrt{r^2+C^2}-C} \]Notice that \( C < 0 \).
-
inline

