Class PenaltyBarrierU_bipower¶
Defined in File PenaltyBarrierU.cc
Inheritance Relationships¶
Base Type¶
public Mechatronix::PenaltyBarrierU_base(Class PenaltyBarrierU_base)
Class Documentation¶
-
class
Mechatronix::PenaltyBarrierU_bipower: public Mechatronix::PenaltyBarrierU_base¶
-
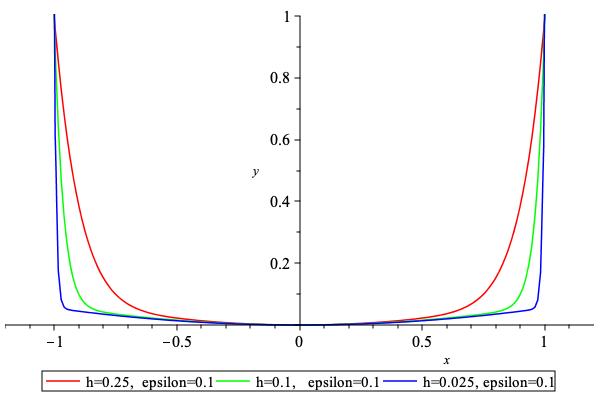
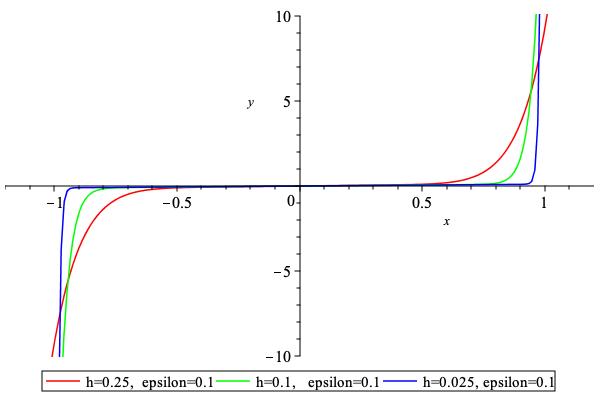
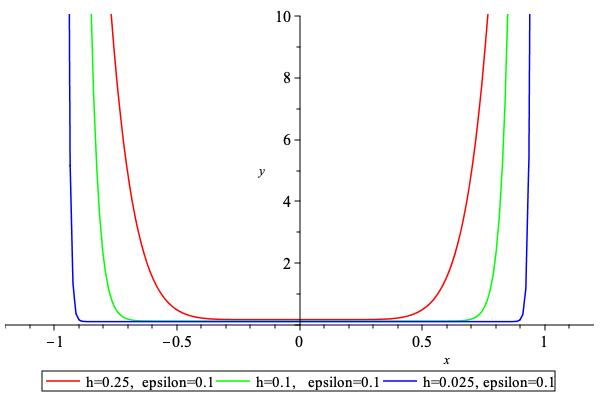
Bipower penalty.
Public Functions
-
inline
PenaltyBarrierU_bipower(string const &name)¶
-
Construct the penalty.
-
inline virtual void
setup(real_type epsilon, real_type tolerance) override¶
-
Initialize the penalty internal parameters based on the values of \( h \) and \( \epsilon \)
Set the parameter
\[ N \geq \frac{\log\left(\frac{\epsilon}{2}\right)} {\log(1-h)} \]where \( N \) is the first even integer which satisfy inequality. Now compute\[ \delta = \frac{\epsilon-(1-h)^N}{(1-h)^2-(1-h)^N} \geq \frac{\epsilon}{2}\]- Parameters
-
epsilon – [in] value \( \epsilon \)
tolerance – [in] value \( h \)
-
inline