Class PosRegularized

• Defined in File Regularized.hh

Inheritance Relationships

Base Type

• public Mechatronix::RegularizedBase (Class RegularizedBase)

Class Documentation

class Mechatronix::PosRegularized : public Mechatronix::RegularizedBase

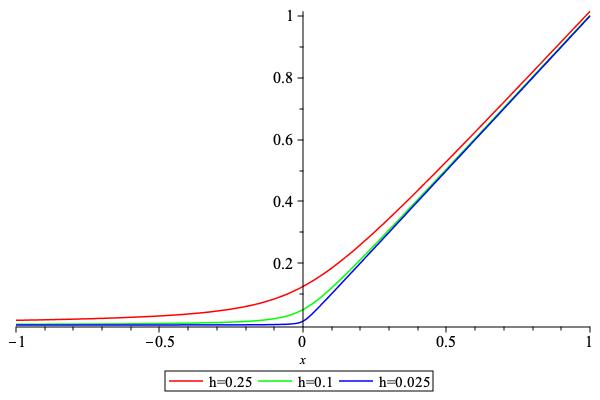
Positive part function smoothed.

Approximate the function

\[\begin{split} \mathrm{pos}(x) = \begin{cases} 0 & x < 0 \\ x & x \geq 0 \end{cases} \end{split}\]

by smoothing function around \(x=0\).

Inizialization

inline explicit PosRegularized()

virtual void setup(GenericContainer const &gc) override

Initialize regularization parameters with a GenericContainer. expect to find gc("h") containing a real scalar

void setup(real_type h)

Initialize regularization parameter h

inline void update_h(real_type h)

Update regularization parameter h

Evaluate

virtual real_type operator()(real_type x) const override

Evaluate positive part regularized:

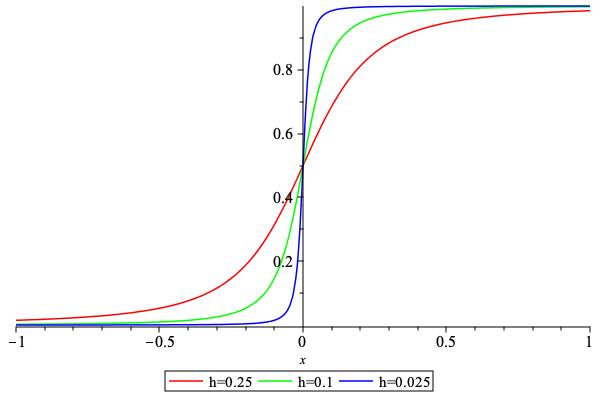
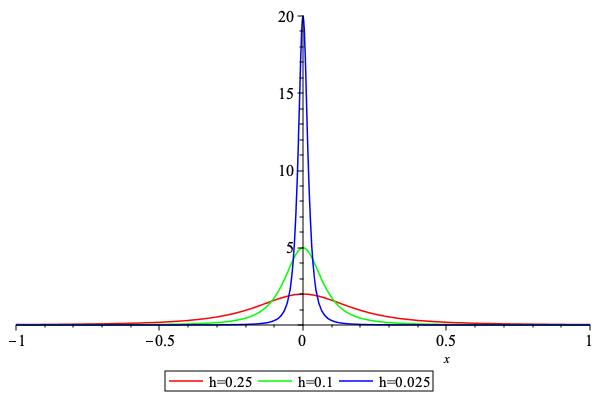
\[\begin{split} \frac{1}{2} \begin{cases} -\displaystyle\frac{\delta^2}{x}\left( 1+\sqrt {1+{\frac{\delta^2}{x^2}}} \right)^{-1} & x < -\delta\\[1em] \delta^2\Big/\left(\sqrt{\delta^2+x^2}-x\right) & x<0\\[1em] \displaystyle\sqrt {\delta^2+x^2}+x & x<\delta \\[1em] x\left( 1+\sqrt{1+{\frac {\delta^2}{x^2}}} \right) & \mathrm{otherwise} \end{cases} \qquad \mathrm{where}\qquad\delta=2h. \end{split}\]

in a stable way.

virtual real_type D(real_type x) const override

First derivative

virtual real_type DD(real_type x) const override

Second derivative

Info

virtual string info() const override