Clip functions

Clip Interval

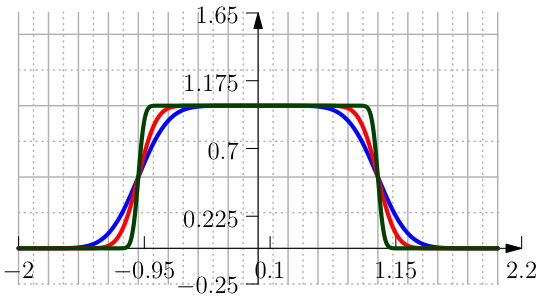
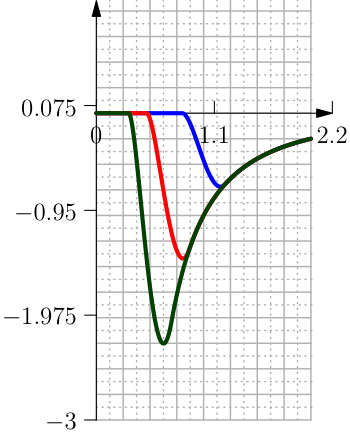
This is the approximation of the characteristic Clip function, which depends on a certain interval \(I=[a,b]\) and returns \(x\) if \(x\in I\), otherwise the result is \(+1\) if \(x>b\) and \(-1\) if \(x<a\).

Clip Interval with erf

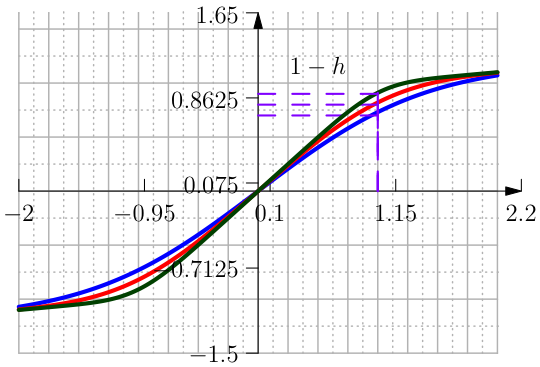
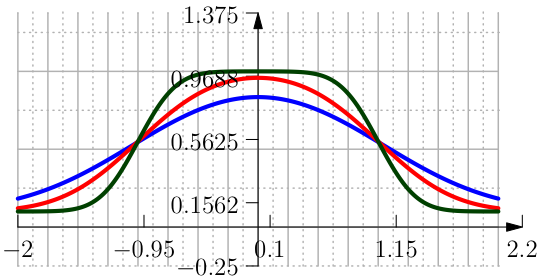
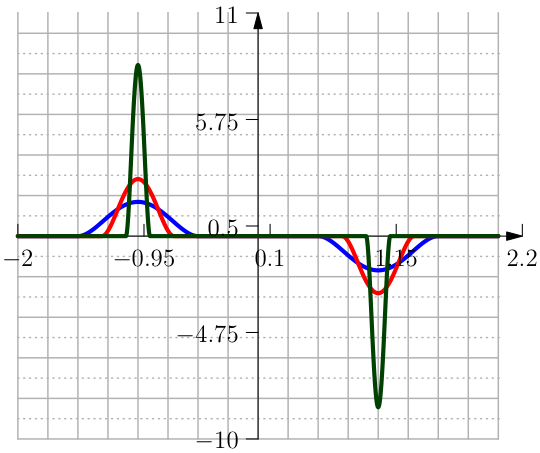
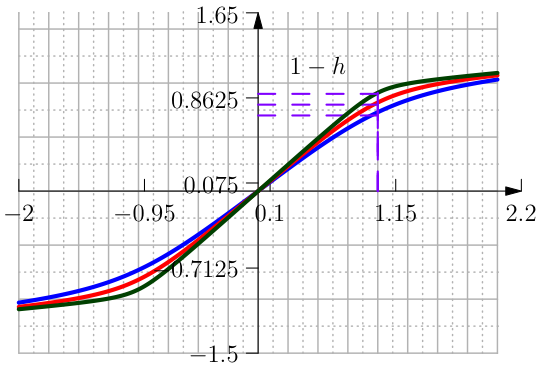
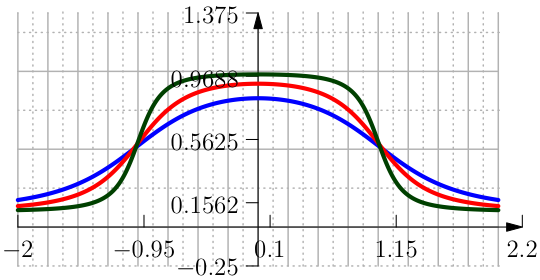
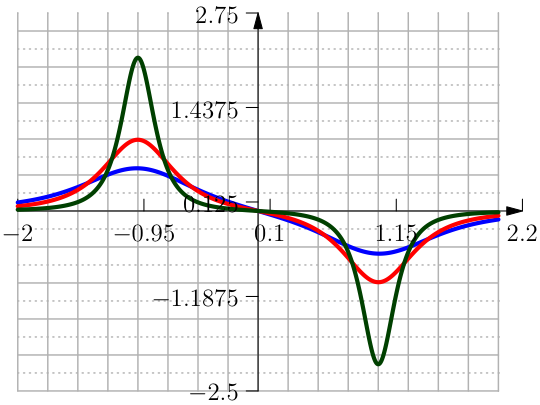
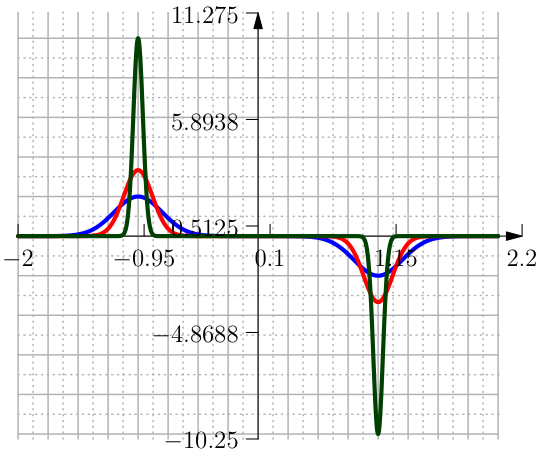
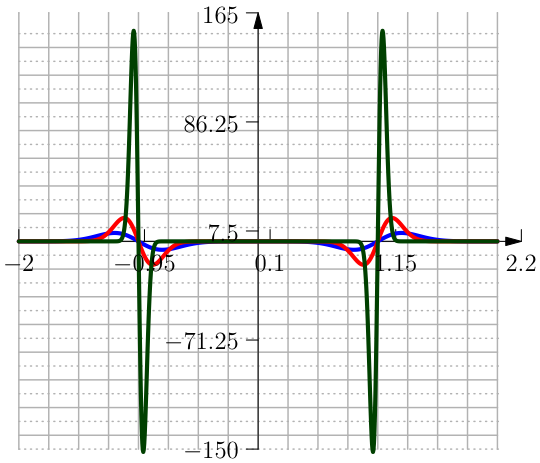
One approximation is done with the Error Function and is defined in terms of \(h\) and \(\delta\) as (see Figure From left to right the function Clip Interval with the \mathrm{erf}, its first and second derivative.).

\[\begin{split}\begin{array}{r@{~}c@{~}l} \mathrm{clip}_{\mathrm{erf}}(x) &=& (1-\delta)f(x)+\delta\, x, \\[1em] f(x) &=& \dfrac{1}{2}\left[ (x+1)\mathrm{erf}(\kappa\,(x+1))-(x-1)\mathrm{erf}(\kappa\,(x-1)) + p(x)\right], \\[1em] p(x)&=& \dfrac{\mathrm{e}^{-\kappa^{2}(x+1)^2} -\mathrm{e}^{-\kappa^2(x-1)^2}} {\kappa\,\sqrt{\pi}}. \end{array}\end{split}\]

The parameter \(\kappa\) is chosen such that \(f(1)=1-h\) therefore

\[\kappa = \dfrac{1}{2h\sqrt{\pi}}.\]

From left to right the function Clip Interval with the \(\mathrm{erf}\), its first and second derivative.

Clip Interval with Polynomials

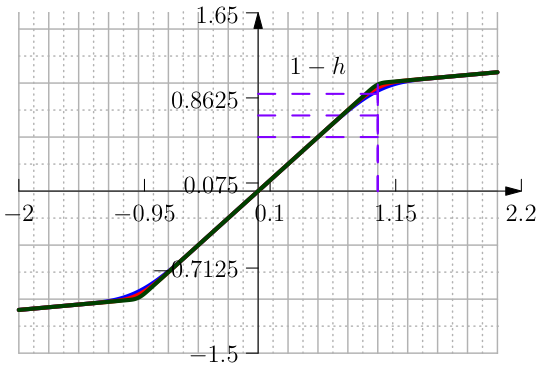
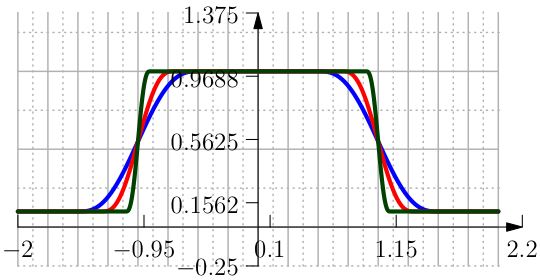
The polynomial approximation of the Clip function in terms of \(h\) and \(\delta\) takes the form of (see Figure From left to right the function Clip Interval with polynomials, its first and second derivative.):

\[\begin{split}\begin{array}{r@{~}c@{~}l} \mathrm{clip}_{\textrm{poly}}(x) &= & (1-\delta)f(x)+\delta\, x,\\[1em] f(x) & = & \begin{cases} -1 & x < -1-h \\[1em] p(x) & x \in[-1-h,-1+h]\\[1em] x & x \in [-1+h,1-h] \\[1em] q(x) & x <\in[1-h,1+h] \\[1em] 1 & x>1+h, \end{cases} \end{array}\end{split}\]

where

\[\begin{split}\begin{array}{r@{~}c@{~}l} p(x) & = & -a+(x+1)(b-(x+1)(c+(x+1)^2(d+e(x+1)^2)))\\[1em] q(x) & = & a+(x-1)(b+(x-1)(c+(x-1)^2(d+e(x-1)^2))). \end{array}\end{split}\]

The coefficients are

\[a = 1-\frac{5h}{32},\quad b = \frac{h}{2},\quad c = -\frac{15h}{32},\quad d = \frac{5h}{32},\quad e = -\frac{h}{32}.\]

From left to right the function Clip Interval with polynomials, its first and second derivative.

Clip Interval with SinAtan

Another possible approximation is with the help of the trigonometric functions \(\sin\) and \(\arctan\). The Clip function can be regularised in terms of \(h\) and \(\delta\) as (see Figure From left to right the function Clip Interval with SinAtan, its first and second derivative.).

\[\begin{split}\begin{array}{r@{~}c@{~}l} \mathrm{clip}_{\textrm{SA}}(x) &=& (1-\delta)f(x)+\delta\, x,\\[1em] f(x) &=& \dfrac{2\kappa x}{\sqrt{1+\kappa^2(x+1)^2}+\sqrt{1+\kappa^2(x-1)^2}}. \end{array}\end{split}\]

The parameters are set so that \(f(1)=1-h\) and hence

\[\kappa = \dfrac{1-h}{h(2-h)}.\]

From left to right the function Clip Interval with SinAtan, its first and second derivative.

Clip Rectangle

A function similar to the Clip function is the Clip Rectangle, which is defined as the characteristic function of an interval, i.e. \(\chi_{[0,1]}(x)\) for the interval \([0,1]\). The critical points are smoothed with the regularisation (see Figure From left to right the function Clip Rectangle, its first and second derivative.):

\[\mathrm{clip}_{\textrm{R}}(x) = \dfrac{\mathrm{erf}(\kappa(1-x))+\mathrm{erf}(\kappa(1+x))}{2},\]

so that \(\mathrm{clip}'_{\textrm{R}}(1)=-1/h\). The value of \(\kappa\) is chosen according to the previous requirement, and is computed numerically with an iterative procedure.

From left to right the function Clip Rectangle, its first and second derivative.

Clip Reciprocal

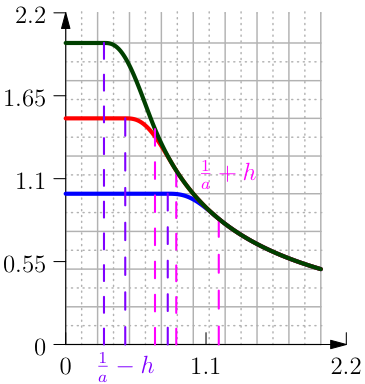
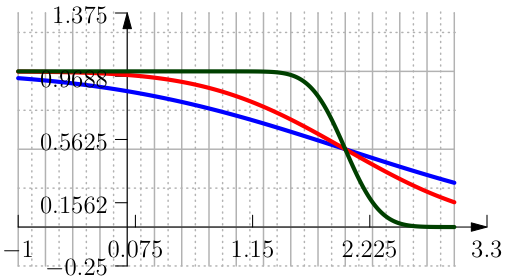
The function Clip Reciprocal (see Figure From left to right the function Clip Reciprocal with its first and second derivative..) is the approximation of the function \(\min(a,1/x)\). The constant \(a\) is given by the user, the parameter \(h\) is the tolerance of:

\[\begin{split}\mathrm{rec}(x) = \begin{cases} a & \textrm{if $x<1/a-h$} \\[1em] a+(x-d)^3(b+c/x) & \textrm{if $x<1/a+h$} \\[1em] 1/x & \textrm{otherwise,} \end{cases}\end{split}\]

with coefficients

\[b = \frac{a}{16\,h^3}, \quad c = -\frac{1+3ah}{16\,h^3}, \quad d = \frac{1}{a}-h.\]

From left to right the function Clip Reciprocal with its first and second derivative..

Clip Superior

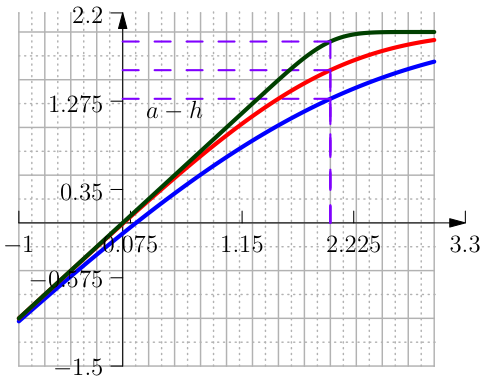
The function Clip Superior is the approximation of the function \(\min(a,x)\). The constant \(a\) is given by the user, the parameter \(h\) is the tolerance of (see Figure From left to right the function Clip Superior with its first and second derivative..):

\[\mathrm{clip}_{\textrm{sup}}(x) = \frac{x+a}{2} -\dfrac{x-a}{2}\textrm{erf}(\kappa(x-a)) -\dfrac{\exp(-\kappa^2(x-a)^2)}{2\kappa\sqrt{\pi}},\]

where \(\kappa\) is chosen to satisfy \(\mathrm{clip}_{\textrm{sup}}(a) =a-h\), and thus} is \(\kappa = \frac{1}{2h\sqrt{\pi}}\).

From left to right the function Clip Superior with its first and second derivative..