Class PenaltyBarrierU¶

Defined in File PenaltyBarrierU.hh

Class Documentation¶

class Mechatronix::PenaltyBarrierU¶

Class for penalize control.

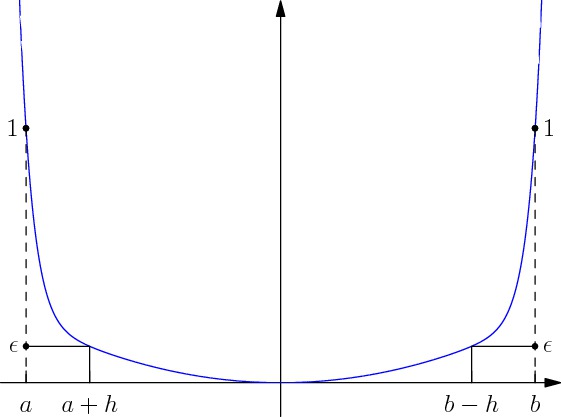
The penalty is defined in the interval \( [a,b] \) with two parameters \( \epsilon \) and \( h \).

The interval \( [a,b] \) is the range where the control must lie.
The parameter \( h \) is the distance from the border of the interval where the penalty start to grow fast.
The parameter \( \epsilon \) is the value of the penalty at distance \( h \) from the border.

../_images/upenalty.jpeg

Public Types

enum [anonymous]¶

Values:

enumerator U_QUADRATIC¶

enumerator U_QUADRATIC2¶

enumerator U_CUBIC¶

enumerator U_QUARTIC¶

enumerator U_PARABOLA¶

enumerator U_LOGARITHMIC¶

enumerator U_COS_LOGARITHMIC¶

enumerator U_TAN2¶

enumerator U_HYPERBOLIC¶

enumerator U_BIPOWER¶

Public Functions

inline explicit PenaltyBarrierU(string const &name)¶: Construct a penalty for control with name name

inline ~PenaltyBarrierU()¶: Destroy the penalty for control.

inline void check_range_throw(real_type u, real_type u_min, real_type u_max) const¶

inline bool check_range(real_type u, real_type u_min, real_type u_max) const¶

void setup(integer type, real_type epsilon, real_type tolerance)¶

build penalty of type type

Build a penalty for the control. The Associative array vars must contain

NAME + “Type” where NAME is the name of the class used in the constructor.
NAME + “Tolerance” the value of \( h \)
NAME + “Epsi” the value of \( \epsilon \)

The possible value of the type are

QUADRATIC: For the penalty PenaltyBarrierU_quadratic
QUADRATIC2: For the penalty PenaltyBarrierU_quadratic_bis
CUBIC: For the penalty PenaltyBarrierU_cubic
QUARTIC: For the penalty PenaltyBarrierU_quartic
PARABOLA: For the penalty PenaltyBarrierU_parabola
LOGARITHMIC: For the barrier PenaltyBarrierU_logarithmic
COS_LOGARITHMIC: For the barrier PenaltyBarrierU_cos_logarithmic
TANGENT2: For the barrier PenaltyBarrierU_tan2
HYPERBOLIC: For the barrier PenaltyBarrierU_hyperbolic
BIPOWER: For the barrier PenaltyBarrierU_bipower

PenaltyBarrierU P("P1");
real_type tolerance  = 0.1;
real_type epsilon    = 0.01;
P.setup( PenaltyBarrierU::QUADRATIC, epsilon, tolerance );

inline void setup(GenericContainer const &GC)¶: build penalty

inline void update_epsilon(real_type epsilon)¶: change the epsilon of the control, used in the continuation

inline void update_tolerance(real_type tolerance)¶: change the tolerance of the control, used in the continuation

inline void info(ostream_type &stream) const¶: print information about the penalty on stream s

inline string info() const¶

inline void save(string const &fname) const¶: save on a file fname the actual penalty values evaluted in the interval [a,b]

inline real_type operator()(real_type x, real_type a, real_type b) const¶: Compute the penalty \( p(x,a,b) \).

inline real_type D_1(real_type x, real_type a, real_type b) const¶: Compute \( \displaystyle\frac{\partial}{\partial_x} p(x,a,b) \).

inline real_type D_2(real_type x, real_type a, real_type b) const¶: Compute \( \partial_a p(x,a,b) \).

inline real_type D_3(real_type x, real_type a, real_type b) const¶: Compute \( \partial_b p(x,a,b) \).

inline real_type D_1_1(real_type x, real_type a, real_type b) const¶: Compute \( \partial_{xx} p(x,a,b) \).

inline real_type D_1_2(real_type x, real_type a, real_type b) const¶: Compute \( \partial_{xa} p(x,a,b) \).

inline real_type D_1_3(real_type x, real_type a, real_type b) const¶: Compute \( \partial_{xb} p(x,a,b) \).

inline real_type D_2_2(real_type x, real_type a, real_type b) const¶: Compute \( \partial_{aa} p(x,a,b) \).

inline real_type D_2_3(real_type x, real_type a, real_type b) const¶: Compute \( \partial_{ab} p(x,a,b) \).

inline real_type D_3_3(real_type x, real_type a, real_type b) const¶: Compute \( \partial_{bb} p(x,a,b) \).

inline real_type solve(real_type RHS, real_type a, real_type b) const¶: Solve the problem \( \displaystyle\frac{\partial}{\partial_x} p(x,a,b) = RHS \).

inline real_type solve_rhs(real_type RHS, real_type a, real_type b) const¶: Given the function \( x(r,a,b) \) defined implicitly as the solution \( \displaystyle\frac{\partial}{\partial_x} p(x(r,a,b),a,b) = r \) compute the derivative \( \partial_r x(r,a,b) \)

inline real_type solve_a(real_type RHS, real_type a, real_type b) const¶: Given the function \( x(r,a,b) \) defined implicitly as the solution \( \displaystyle\frac{\partial}{\partial_x} p(x(r,a,b),a,b) = r \) compute the derivative \( \partial_a x(r,a,b) \)

inline real_type solve_b(real_type RHS, real_type a, real_type b) const¶: Given the function \( x(r,a,b) \) defined implicitly as the solution \( \displaystyle\frac{\partial}{\partial_x} p(x(r,a,b),a,b) = r \) compute the derivative \( \partial_b x(r,a,b) \)

Protected Functions

real_type getTolerance(GenericContainer const &GC) const¶

real_type getEpsilon(GenericContainer const &GC) const¶

integer getType(GenericContainer const &GC) const¶

Protected Attributes

string const m_name¶: name of the penalty

PenaltyBarrierU_base *m_pPenalty¶: pointer to the true used penalty